This comprehensive guide provides a structured approach to understanding angles in triangles, focusing on key concepts, practical applications, and intervention strategies to master angle properties effectively.
1.1 Overview of the Study Guide

This study guide is designed to provide a clear and structured approach to understanding angles in triangles. It covers foundational concepts, properties, and practical applications, ensuring a comprehensive learning experience. The guide is divided into sections that progress from basic angle definitions to advanced topics, including real-world applications and intervention strategies. Each chapter builds on previous knowledge, making it easier to grasp complex ideas. The guide emphasizes problem-solving techniques and critical thinking, supported by interactive activities and technological tools. By following this guide, learners will gain a deep understanding of angle properties and their significance in various fields, preparing them for advanced mathematical studies and practical challenges.
1.2 Importance of Understanding Angles in Triangles
Understanding angles in triangles is fundamental for building a strong foundation in geometry and trigonometry. Angles determine the shape and properties of triangles, influencing their applications in various fields such as architecture, engineering, and navigation. Grasping angle concepts enables problem-solving in real-world scenarios, like calculating heights, distances, and structural integrity. Additionally, angles are crucial in advanced mathematical theories, including polygon angle sum theorems and trigonometric functions. Mastery of angle properties fosters critical thinking and analytical skills, essential for academic and professional success. This knowledge also enhances spatial reasoning, benefiting fields like design and physics. Thus, understanding angles is not just academic—it’s a practical tool for navigating the world.
1.3 Objectives of the Study Guide
The primary objective of this study guide is to provide a comprehensive understanding of angle properties and their applications in triangles. It aims to equip students with the skills to classify triangles based on angles, solve for unknown angles using various properties, and apply these concepts in real-world scenarios. The guide also focuses on addressing common misconceptions and reinforcing learning through interactive activities and technology. By the end of this guide, students should be able to demonstrate a deep understanding of angle relationships, utilize supplementary and complementary angles effectively, and confidently tackle complex geometric problems. Additionally, the guide serves as a foundation for advanced topics in trigonometry and polygon angle theorems.
Basic Concepts of Angles
Angles are formed by two rays sharing a common endpoint, measured in degrees. They can be acute, obtuse, right, straight, or reflex, each with specific properties.
2.1 Definition and Types of Angles
An angle is formed by two rays sharing a common endpoint. Angles are measured in degrees, ranging from 0° to 360°, and are classified based on their degree measurements. The primary types include:
- Acute angles: Less than 90°, commonly found in triangles and geometric shapes.
- Obtuse angles: Greater than 90° but less than 180°, often seen in larger polygons.
- Right angles: Exactly 90°, forming a square corner.
- Straight angles: 180°, forming a straight line.
- Reflex angles: Greater than 180° but less than 360°, used in advanced geometric analysis.
Understanding these classifications is essential for solving problems involving angles in triangles and other geometric figures.
2.2 Measuring Angles in Degrees
Angles are measured in degrees, with a full circle equal to 360°. The degree system divides a circle into 360 equal parts, allowing precise measurement of angles. A protractor is commonly used to measure angles, with markings from 0° to 180° on both sides. To measure an angle:
- Align the protractor’s baseline with one side of the angle.
- Ensure the vertex of the angle is at the center of the protractor.
- Read the measurement where the other side intersects the protractor’s scale.
Understanding degree measurements is fundamental for analyzing angles in triangles and solving geometric problems effectively.
2.3 Acute, Obtuse, Right, Straight, and Reflex Angles
Angles are classified based on their degree measurements. An acute angle measures less than 90°, while an obtuse angle measures between 90° and 180°. A right angle is exactly 90°, often seen in rectangles and squares. A straight angle measures 180°, forming a straight line. Beyond this, a reflex angle measures more than 180° but less than 360°, commonly found in shapes like chevrons or arrowheads. These classifications are essential for analyzing triangles and solving geometric problems effectively. Understanding these angle types helps in identifying triangle types and applying angle properties in real-world applications.

Properties of Angles in Triangles
This section explores the fundamental properties of angles within triangles, including the sum of interior angles, characteristics of different triangle types, and the relationship between angles and sides.
3.1 Sum of Interior Angles in a Triangle
A fundamental property of triangles is that the sum of their interior angles always equals 180 degrees. This principle applies universally to all triangles, whether they are acute, right-angled, or obtuse. Understanding this concept is crucial for solving problems involving triangle angle relationships. By grasping this basic property, students can better comprehend more complex geometric principles. This section delves into the reasoning behind this consistent sum and its practical applications in various mathematical problems. Mastery of this concept is essential for progressing in geometry and related fields, as it forms the foundation for analyzing triangle properties and solving real-world problems.
3;2 Properties of Equilateral, Isosceles, and Scalene Triangles
Understanding the properties of equilateral, isosceles, and scalene triangles is essential for mastering angle relationships. An equilateral triangle has all sides equal and all interior angles measuring 60 degrees, making it highly symmetrical. An isosceles triangle features two equal sides and two equal angles, with the third angle differing. In contrast, a scalene triangle has all sides of different lengths and all angles unique. These classifications are fundamental in geometry, aiding in problem-solving and analyzing real-world shapes. By recognizing these properties, students can better classify triangles and apply their knowledge to practical applications, enhancing their understanding of geometric principles and angle relationships.
3.3 Relationship Between Angles and Sides in a Triangle
The relationship between angles and sides in a triangle is a cornerstone of geometry. In any triangle, the larger angle is opposite the longer side, and conversely, the longer side is opposite the larger angle. This principle, known as the Angle-Side Relationship, helps determine the type of triangle and predicts its properties. For example, in an equilateral triangle, all angles and sides are equal. In an isosceles triangle, the equal sides correspond to the equal angles. Understanding this relationship is crucial for solving problems involving triangle classification, construction, and trigonometry. By mastering this concept, students can apply it to various geometric scenarios, enhancing their analytical skills and problem-solving abilities in mathematics. This fundamental relationship is essential for advancing in geometry and related fields.

Types of Triangles Based on Angles
Triangles are classified as acute (all angles <90°), right (one 90° angle), or obtuse (one angle >90°), based on their angle measurements.
4.1 Acute, Right, and Obtuse Triangles
Triangles are categorized based on their angles: acute (all angles less than 90°), right (one 90° angle), and obtuse (one angle greater than 90°). These classifications help in understanding geometric properties. Acute triangles are versatile, while right triangles are fundamental in trigonometry. Obtuse triangles often involve supplementary angles. Each type has unique applications in fields like construction and navigation, making their identification crucial. This section explores their definitions, examples, and real-world uses, emphasizing the importance of angle measurements in triangle classification.
4.2 Classifying Triangles by Angles and Sides
Classifying triangles involves analyzing both their angles and sides. By angles, triangles are categorized as acute, right, or obtuse. By sides, they are classified as equilateral, isosceles, or scalene. This dual classification system provides a deeper understanding of their properties. For example, an equilateral triangle is also an acute triangle, while a scalene triangle can be acute, right, or obtuse. Mastering this classification is essential for solving geometric problems and understanding real-world applications, such as designing structures or calculating distances. This section explores the intersection of angle and side classifications, offering practical examples to reinforce these concepts.
4.3 Special Properties of Right-Angled Triangles
Right-angled triangles possess unique properties that make them fundamental in geometry. The presence of a 90-degree angle distinguishes them, and the Pythagorean theorem (a² + b² = c²) applies, where c is the hypotenuse. These triangles also exhibit trigonometric relationships, such as sine, cosine, and tangent, which are essential for calculating unknown sides and angles. Additionally, right-angled triangles are integral in real-world applications like engineering, physics, and navigation. Their properties simplify complex calculations, making them a cornerstone of problem-solving in various fields. Understanding these special characteristics is crucial for advanced mathematical studies and practical problem-solving scenarios.
Relationships Between Angles
Understanding angle relationships, such as supplementary (180°), complementary (90°), corresponding, alternate interior, and alternate exterior angles, is crucial for solving geometric problems and real-world applications.
5.1 Supplementary and Complementary Angles
Supplementary angles sum to 180°, forming a straight line, while complementary angles add up to 90°, creating a right angle. Both relationships are essential in geometry for solving problems involving angles in triangles, parallel lines, and polygons. Supplementary angles are often encountered in triangle exterior angle theorems, while complementary angles are key in right-angled triangles. Understanding these concepts helps in calculating unknown angles, verifying angle sums, and applying properties in real-world scenarios like architecture and engineering. For example, if one angle in a pair of supplementary angles is 120°, the other must be 60°. These relationships provide foundational tools for advanced geometric problem-solving.
5.2 Corresponding, Alternate Interior, and Alternate Exterior Angles
Corresponding angles are equal when two lines intersect, while alternate interior and alternate exterior angles are equal when a transversal crosses parallel lines. These angle relationships are fundamental in geometry, particularly in proving properties of parallel lines and triangles. Corresponding angles are identical due to vertical angles formed by intersecting lines. Alternate interior angles are on opposite sides of the transversal and inside the parallel lines, while alternate exterior angles are on opposite sides but outside. These concepts are essential for solving problems involving angles in triangles, parallelograms, and real-world applications like designing stable structures in architecture. Understanding these relationships enhances spatial reasoning and problem-solving skills.
5.3 Vertical Angles and Linear Pairs
Vertical angles are formed when two lines intersect, creating pairs of equal angles opposite each other. These angles are always equal in measure. Linear pairs, on the other hand, are adjacent angles that form a straight line, summing to 180 degrees. Understanding these concepts is crucial for solving problems in geometry, particularly in triangles and parallel lines. Vertical angles and linear pairs often work together in supplementary relationships, aiding in angle sum calculations. Mastery of these properties enhances problem-solving skills in various geometric contexts, including architecture and engineering, where precise angle measurements are essential for designing stable structures and ensuring safety.
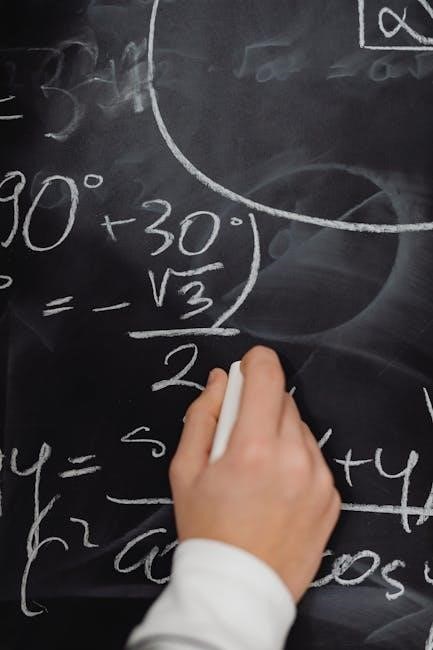
Solving for Unknown Angles
Mastering techniques to find unknown angles involves using angle sum properties, exterior angle theorems, and supplementary relationships. These strategies are essential for solving triangle problems accurately and efficiently.
6.1 Using Angle Sum Property in Triangles
The angle sum property states that the sum of the interior angles in any triangle is always 180 degrees. This fundamental concept is crucial for solving unknown angles; By knowing two angles, the third can be calculated by subtracting their sum from 180 degrees. This method is particularly useful in equilateral, isosceles, and scalene triangles. For example, in a triangle with angles 60° and 70°, the third angle is 50° (180 ⸺ 60, 70). This property simplifies problem-solving and enhances understanding of triangle angle relationships. Regular practice using this property helps build a strong foundation in geometry and prepares students for advanced concepts like trigonometry and polygon angle calculations.
6.2 Solving for Exterior Angles of a Triangle
An exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. To find an exterior angle, subtract the adjacent interior angle from 180 degrees. For example, if an interior angle is 60°, the exterior angle is 120° (180 — 60). This relationship is derived from the supplementary angle property; The sum of all exterior angles in any triangle is always 360 degrees, regardless of the triangle type. Understanding exterior angles enhances problem-solving skills and is essential for advanced geometry concepts. Regular practice with real-world examples helps solidify this property and its applications in various mathematical scenarios.

6.3 Applying Supplementary and Complementary Angle Relationships
Supplementary angles add up to 180°, while complementary angles sum to 90°. In triangles, these relationships are crucial for solving unknown angles. For example, if two angles in a triangle are known, the third can be found using the supplementary property (sum of angles = 180°). Similarly, complementary relationships are useful in right-angled triangles, where the two non-right angles must add to 90°. Applying these concepts helps in solving for exterior angles and understanding angle properties. Regular practice and real-world applications reinforce these fundamental principles, making them indispensable for advanced geometric problem-solving and fostering a deeper understanding of spatial relationships in various mathematical contexts. These relationships are foundational to trigonometry and other higher-level studies.

Real-World Applications of Angle Properties
Angle properties are essential in architecture, engineering, and navigation, enabling precise designs, stable structures, and accurate triangulation, demonstrating their practical relevance beyond theoretical mathematics.
7.1 Angles in Architecture and Engineering
Understanding angle properties is crucial in architecture and engineering, as they form the foundation for designing stable and aesthetically pleasing structures. Architects use right angles, acute angles, and obtuse angles to create functional and visually appealing buildings. For instance, right angles are essential for constructing square or rectangular frames, while acute and obtuse angles add complexity to designs. Engineers rely on angle calculations to ensure the structural integrity of bridges, dams, and skyscrapers. The precise measurement and application of angles ensure that buildings can withstand external forces like wind and earthquakes. Additionally, geometric principles, such as complementary and supplementary angles, are applied in creating symmetrical and balanced designs, enhancing both functionality and beauty in construction projects.
7.2 Using Triangle Angle Properties in Navigation
Triangle angle properties play a vital role in navigation, particularly in determining direction, distance, and location. Triangulation, a method used in navigation, relies on the measurement of angles to calculate distances and positions; By understanding concepts like supplementary and complementary angles, navigators can determine precise bearings and courses. For instance, right angles are essential in mapping coordinate systems, while acute and obtuse angles help in plotting trajectories. Additionally, the angle sum property of triangles is used in GPS technology to pinpoint locations accurately. These geometric principles are fundamental in aviation, maritime, and terrestrial navigation, ensuring safe and efficient travel. Mastery of angle relationships enhances navigational accuracy and reliability in various real-world applications.
7.3 Practical Problem-Solving with Angles
Understanding angle properties is crucial for practical problem-solving in various fields. In real-world scenarios, such as construction or engineering, identifying and applying angle relationships can lead to efficient solutions. For instance, determining the correct angles for a roof slope or bridge design ensures structural integrity. Problem-solving strategies like using the angle sum property or supplementary angles can simplify complex calculations. Additionally, interactive activities and visual tools help learners grasp these concepts intuitively. By mastering angle properties, individuals can approach problems with confidence, ensuring accuracy and creativity in their solutions. This skill is invaluable in both academic and professional settings, fostering critical thinking and innovation.

Intervention Strategies for Understanding Angles
Intervention strategies include interactive activities, technology tools, and addressing misconceptions to help students grasp angle concepts effectively, ensuring a strong foundation for advanced geometry topics.
8.1 Addressing Common Misconceptions About Angles
Common misconceptions about angles often stem from students’ difficulty in distinguishing between acute, obtuse, and right angles. Some may believe that all triangles have a right angle, while others confuse supplementary and complementary relationships. To address these, educators can use interactive activities, such as angle classification games and real-world applications, to clarify concepts. Technology tools, like geometric software, can also help students visualize and explore angle properties. Additionally, discussing historical contributions to angle theories can provide context and deepen understanding. By targeting these areas, teachers can help students build a stronger foundation in angle properties and their practical applications.
8.2 Interactive Activities for Learning Angle Properties
Interactive activities are essential for engaging students and reinforcing angle properties. Hands-on exercises, such as constructing triangles with geoboards or identifying angles in real-world objects, encourage active learning. Digital tools like angle simulation software can provide visual representations of angle relationships. Group activities, such as angle sorting games or collaborative puzzles, foster teamwork and discussion. Incorporating games like “Angle Bingo” or “Pin the Angle” adds fun while reinforcing concepts. These activities help students connect theoretical knowledge to practical applications, making learning more enjoyable and effective. By integrating technology and creativity, educators can cater to diverse learning styles and enhance understanding of angle properties in triangles.
8.3 Using Technology to Reinforce Angle Concepts
Technology plays a vital role in enhancing the understanding of angle properties through interactive and visual tools. Online platforms offer simulations where students can manipulate angles in real-time, observing how changes affect triangle properties. Educational apps provide step-by-step solutions and quizzes to test knowledge. Virtual labs allow experimentation with angles in various geometric shapes, making complex concepts more accessible. Additionally, video tutorials and animated lessons can break down challenging topics into digestible parts. These resources cater to different learning styles and provide personalized learning experiences. By integrating technology, educators can create engaging and effective environments for mastering angle properties, ensuring deeper comprehension and retention of the material.

Advanced Topics in Triangle Angles
Explore advanced concepts like polygon angle sum theorem, trigonometric relationships, and historical contributions to angle theories, expanding understanding beyond basic triangle properties.
9.1 Exploring Polygon Angle Sum Theorem
The polygon angle sum theorem states that the sum of interior angles of an n-sided polygon is given by the formula ((n-2) imes 180^ rc). This theorem extends beyond triangles, providing a foundational concept for understanding more complex shapes. For example, a quadrilateral (4 sides) has an interior angle sum of (360^ rc), while a pentagon (5 sides) sums to (540^ rc). This theorem is crucial for solving problems involving various polygons and their properties. It also finds applications in real-world scenarios, such as architecture and engineering, where understanding spatial relationships is essential. By mastering this theorem, students can better grasp geometric principles and their practical applications.
Trigonometry is a branch of mathematics that explores the relationships between angles and sides of triangles. It introduces essential functions like sine, cosine, and tangent, which are crucial for solving problems in various fields. Understanding angle relationships, such as supplementary and complementary angles, forms the foundation of trigonometric principles. This section delves into how these concepts extend beyond basic geometry, offering practical applications in navigation, physics, and engineering. By mastering trigonometric identities and graphs, students can tackle complex problems involving periodic phenomena and spatial analysis. This introduction to trigonometry bridges the gap between angle properties and their real-world applications, setting the stage for advanced mathematical exploration.
9.3 Historical Contributions to Angle Theories
The study of angles and triangles has been shaped by contributions from ancient civilizations and renowned mathematicians. Early Babylonian and Egyptian mathematicians laid the groundwork for geometric principles. Greek scholars like Euclid and Pythagoras further developed these concepts, establishing theorems that remain foundational. During the Islamic Golden Age, mathematicians such as Al-Battani expanded trigonometric understanding. In the Renaissance, figures like Copernicus and Galileo bridged geometry with astronomy. These historical advancements not only refined angle theories but also paved the way for modern applications in various fields. Understanding this historical context enriches the appreciation of angle properties and their role in shaping mathematics and science.

This study guide has provided a thorough exploration of angle properties in triangles, offering practical strategies and real-world applications. Further learning resources are available for continued growth.
10.1 Summary of Key Concepts
This study guide has covered essential topics related to angles in triangles, including their properties, classifications, and real-world applications; Key concepts such as the sum of interior angles, types of triangles based on angles, and supplementary and complementary relationships were explored. Intervention strategies, including interactive activities and technology tools, were highlighted to enhance learning. Practical problem-solving techniques and the importance of understanding angle properties in various fields like architecture and navigation were emphasized. The guide also provided resources for further learning and encouraged applying angle knowledge in future studies. By mastering these concepts, students can build a strong foundation for advanced mathematical topics.
10.2 Resources for Further Learning
For deeper understanding, utilize textbooks like Math Ready and online platforms offering interactive geometry tools. Websites such as Khan Academy and GeoGebra provide tutorials and exercises. Additionally, educational apps like Desmos and CK-12 offer dynamic resources for visualizing angle properties. Join online forums and study groups for peer support and shared problem-solving; Consult teacher guides for tailored intervention strategies and enrichment materials. Local libraries often have math workbooks and study guides focused on triangles and angles. Engage with educational YouTube channels for video explanations and real-world applications. Lastly, explore research papers on polygon angle theorems for advanced insights. These resources will enhance your mastery of angle concepts and their practical uses.
10.3 Applying Angle Knowledge in Future Studies
Mastering angle properties in triangles lays a strong foundation for advanced mathematics, including trigonometry, geometry, and engineering. Understanding these concepts aids in solving complex problems in STEM fields. The ability to classify triangles and calculate angles is crucial for architecture and design. Additionally, knowledge of angle relationships enhances spatial reasoning and analytical thinking, benefiting future studies in physics and computer science. By grasping these principles, students can approach challenges in navigation, surveying, and even art with confidence. This foundational understanding also supports learning polygon angle theorems and advanced geometric principles. Applying angle knowledge fosters problem-solving skills essential for academic and real-world success, making it a versatile tool for lifelong learning.





